Fonctions

Dérivée

Introduction

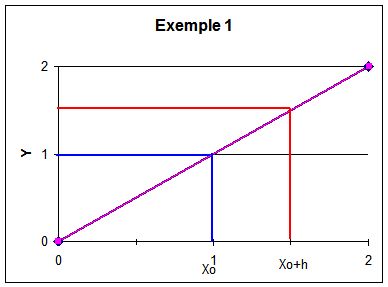
Définition du nombre dérivé

Soit f une fonction définie sur un intervalle I, non réduit à un point, et contenant x₀.

Soit h un réel tel que x₀ + h appartienne à I.

La fonction f est dite dérivable en x₀

si la fonction admet une limite finie quand h tend vers zéro.

Cette limite est alors appelée nombre dérivé de f en x₀ et est noté : f’(x₀).

Dérivée sur un intervalle : définition

Soit I un intervalle non réduit à un point. Soit f une fonction définie sur I.

On dit que la fonction f est dérivable sur I si elle est dérivable en tout point de I.

Quelques dérivées

Soient u et v deux fonctions dérivables sur un intervalle I, u’ et v’ leurs fonctions dérivées respectives. Alors :

Fonction	Fonction dérivée
u + v	u’ + v’
au (a réel)	au’
u^α(α rationnel)	α u^α-1u’
uv	u’v + uv’
(u(x) ≠ 0)
(v(x) ≠ 0)
(u(x) > 0)

Application à l’étude du comportement global des fonctions

Si f est dérivable sur un intervalle I non réduit à un point, et admet un maximum local (ou un minimum local) en un point a distinct des extrémités de I, alors f’(a) = 0.

Si f est dérivable sur un intervalle I non réduit à un point et si la dérivée f’ est nulle sur I, alors f est constante sur I.

Si f est dérivable sur un intervalle I non réduit à un point, et si f’ est positive sur I, alors f est croissante sur I.

Si f est dérivable sur un intervalle I non réduit à un point, et si f’ est négative sur I, alors f est décroissante sur I.

Autres applications de la dérivée

Résolution d’équations et d’inéquations

Déterminer une tangente

Calculs approchés

Calcul de coût marginal…

Fonctions logarithmes

« A quoi ça sert ? »

On place 2 000 € sur un compte au taux de 8,5 % l'an (intérêts composés).

1) Au bout de 10 ans, quel capital y aura t-il sur le compte?

2) Déterminer au bout de combien d'années le capital aura dépassé 20 000 €.

Tracé de la fonction logarithme népérien

Tableau de valeurs et tracé de la fonction

x	- 1	0,1	0,5	0,8	0,9	1	1,1	1,2	2	3	4
ln x

Quelques propriétés

La fonction ln est définie sur ] 0 , +¥ [ .

ln 1 =

Elle est dérivable sur ] 0 , +¥ [ . ( ln x)’ = 1/x

Soit u une fonction dérivable et strictement positive sur un intervalle I. Alors,

la fonction ln u est dérivable sur I et sa dérivée est (ln u)’ =

Tableau de variations

x	0 +¥
( ln x )'
ln x

Le nombre e :

ln e = 1

Propriétés fondamentales

a et b étant strictement positifs, r étant un rationnel ( exemple : 3/2 , -4/9, -6, mais pas ):

ln ( ab ) =
ln ( a/b ) =
ln ( 1/a ) =
ln ( a^r ) =

La fonction logarithme décimal

Elle est définie sur ] 0 , +¥ [ par : log x =

log 10 = log 10^r = pour r rationnel.

Fonctions exponentielles

Introduction

Plaçons 2 000 € sur un compte au taux de 8,5 % l’an (intérêts composés).

Au bout de t années, quelle est la valeur du capital ?

Fonctions exponentielles : tracé de quelques courbes

Remplir le tableau de valeurs et tracer les courbes

X	-4	-3	-2	-1	0	1	2	3	4	5
e^x
2^x
0,5^x

La fonction x |® a^x (a > 0)

Définition :

a^x = e^xlna

1^er cas : a > 1

Exemples : 2^x, e^x

Courbe :

2^ème cas : 0 < a <1

Exemple : 0,5^x

Courbe :

Fonction logarithme et fonction exponentielle

x |® e^x est la fonction réciproque de la fonction logarithme népérien.

La fonction exponentielle est définie sur l’ensemble des réels et prend ses valeurs dans ]0 ;+¥[.

Pour tout x réel et tout y strictement positif :

y = e^x équivaut à x = ln y

Ainsi :

Pour tout x réel ln e^x =

Pour tout x strictement positif : e^{ln x} =

Quelques propriétés de la fonction exponentielle

e¹ = e⁰ =

Pour tous réels a et b, tout entier p,

e^a+b = e^-a =

e^a-b = (e^a)^p=

Dérivée : (e^x)’ = (a^x)’ =

Limites

U étant une fonction définie et dérivable sur un intervalle I, la fonction e^u est dérivable sur I et on a (e^u)’ = u’ × e^u