Matrices à coefficients réels

Notions de calcul matriciel

Situation

Une entreprise a reçu commande de 3 clients Marc, Pierre et François. Les commandes concernent des marchandises qui peuvent être fournies par 2 entreprises que nous appellerons A et B :

Quantités commandées	Par clients
	Marc	Pierre	François
à l'usine A	10	12	20
à l'usine B	3	25	10

Les commandes sont exécutées. Pour chaque client l'entreprise a calculé le coût unitaire de revient de la marchandise livrée, et elle a facturé chaque article à un certain prix de vente unitaire :

	Prix unitaire
	Prix de revient	Prix de vente
Marc	20	30
Pierre	15	20
François	40	50

Problème : compléter le tableau suivant :

	Chiffres d'affaires
	Prix de revient	Prix de vente
Usine A
Usine B

Exemples de matrices

Matrice identité :

Ecriture d’une matrice

Exemple

Matrice comportant 4 lignes et 3 colonnes :

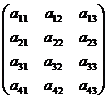
Cas général 

Multiplication ou division d'une matrice par un nombre

Exemples

Règle

Pour multiplier (respectivement diviser) une matrice par un nombre, on multiple (respectivement divise) chaque terme de la matrice par ce nombre.

Addition et soustraction de 2 matrices

Exemples

Règle

On additionne ( respectivement soustrait ) 2 à 2 les termes homologues.

Les deux matrices doivent avoir le même nombre de lignes, et le même nombre de colonnes.

Produit de 2 matrices

Retour à la situation

Quantités commandées	Par clients
	Marc	Pierre	François
à l'usine A	10	12	20
à l'usine B	3	25	10

Traduction matricielle : M =

	Prix unitaire
	Prix de revient	Prix de vente
Marc	20	30
Pierre	15	20
François	40	50

Traduction matricielle : N =

Compléter le tableau suivant :

	Chiffres d'affaires
	Prix de revient	Prix de vente
Usine A
Usine B

Traduction matricielle : R =

Calculs matriciels :

Règle

Lorsqu’on effectue le produit d’une matrice A par une matrice B,

le nombre de colonnes de la matrice A doit être égal au nombre de lignes de la matrice B.

Exemples 

Calculer A ´ B, puis B ´ A. Conclusion.

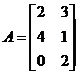
Résoudre un système linéaire à l’aide des matrices

Situation

Dans un magasin de bricolage, trois clients font des achats :

Le client A achète pour 314 € : 8 rouleaux de papier peint

3 kg de peinture

1 kg d'apprêt.

Le client B achète pour 225 € : 5 rouleaux de papier peint

2 kg de peinture

2 kg d'apprêt.

Le client C achète pour 478 € : 12 rouleaux de papier peint

5 kg de peinture

1 kg d'apprêt.

Déterminer le prix du rouleau de papier peint, du kilo de peinture et du kilo d'apprêt.

Utiliser la méthode matricielle de résolution des systèmes.

Mettre sous forme matricielle le système :

Ce système équivaut à : AX = B où :

A = X = B =

Calcul de X :

L’inverse d’une matrice

Définitions

On appelle matrice carrée d’ordre n une matrice ayant n lignes et n colonnes.

Une matrice carrée A d’ordre n est dite inversible s’il existe une matrice A’ telle que AA’ = A’A = I_n

Dans ce cas, on dit que A^-1 = A’

Exemple

Considérons

Cette matrice est inversible : A^-1 existe.

Cherchons son inverse.

Écrivons l’équation matricielle A X = Y avec 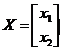et

A^-1 sera déterminée par X = A^-1 Y

A vous

Considérons

Cette matrice est inversible : A^-1 existe.

Chercher son inverse.

Retour à la situation

Notions sur le déterminant d’une matrice

Définition

On appelle matrice carrée d’ordre n une matrice ayant n lignes et n colonnes.

La notion de déterminant ne concernera que les matrices carrées.

Déterminant d’une Matrice 2´2

Exemple

Calculer det A, dans le cas où

Règle

det A = a₁₁ ´ a₂₂ – a₂₁ ´ a₁₂

A vous

Calculer

Déterminant d’une Matrice 3´3

Exemple

Calculer det A, dans le cas où

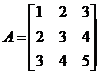
Règle

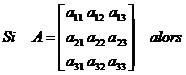
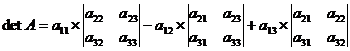
A vous

Calculer det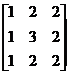

Déterminant du Produit de deux matrices

Exemple d’introduction

1. Calculer , puis le déterminant de cette matrice.

2. Calculer

Règle

A vous

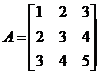
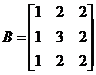
Calculer

Déterminant de l’inverse d’une matrice

Exemple

A =

Calculer le déterminant de l’inverse de A

Règles

Si le déterminant de la matrice A est non nul, alors :

Propriété

Une matrice carrée d’ordre n est inversible si et seulement si son déterminant est non nul

A vous

Calculer le déterminant de l’inverse de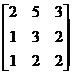

Quelques propriétés

Si une matrice a deux lignes égales, son déterminant est nul.

Un déterminant est nul si et seulement si l’une des lignes est combinaison linéaire des autres lignes.

Si on échange entre elles deux lignes, le déterminant change de signe.

Les propriétés affirmées pour les lignes peuvent être affirmées pour les colonnes.

Exemple du cours

A X = B où :

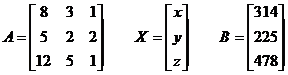
Le problème revient à chercher X tel que X = A^-1 B

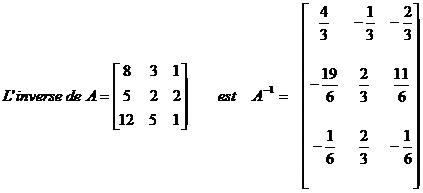
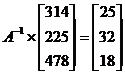
Ainsi :
x = 25 y = 32 z = 18

Conclusion : le prix du rouleau de papier peint est : 25 €,
du kilo de peinture : 32 €,
du kilo d'apprêt : 18 €.